History of Mathematics
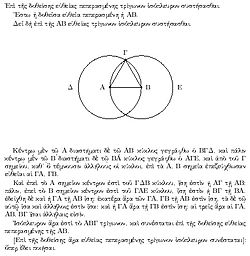
A proof from Euclid's Elements, widely considered the most influential textbook of all time.
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past.
Before the modern age and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. The most ancient mathematical texts available are Plimpton 322 (Babylonian mathematics c. 1900 BC), the Rhind Mathematical Papyrus (Egyptian mathematics c. 2000-1800 BC) and the Moscow Mathematical Papyrus (Egyptian mathematics c. 1890 BC). All of these texts concern the so-called Pythagorean theorem, which seems to be the most ancient and widespread mathematical development after basic arithmetic and geometry.
The study of mathematics as a subject in its own right begins in the 6th century BC with the Pythagoreans, who coined the term "mathematics" from the ancient Greekμάθημα (mathema), meaning "subject of instruction". Greek mathematics greatly refined the methods (especially through the introduction of deductive reasoning and mathematical rigor in proofs) and expanded the subject matter of mathematics. Chinese mathematics made early contributions, including a place value system. The Hindu-Arabic numeral system and the rules for the use of its operations, in use throughout the world today, likely evolved over the course of the first millennium AD in India and was transmitted to the west via Islamic mathematics. Islamic mathematics, in turn, developed and expanded the mathematics known to these civilizations. Many Greek and Arabic texts on mathematics were then translated into Latin, which led to further development of mathematics in medieval Europe.
From ancient times through the Middle Ages, bursts of mathematical creativity were often followed by centuries of stagnation. Beginning in Renaissance Italy in the 16th century, new mathematical developments, interacting with new scientific discoveries, were made at an increasing pace that continues through the present day.
A proof from Euclid's Elements, widely considered the most influential textbook of all time.
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past.
Before the modern age and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. The most ancient mathematical texts available are Plimpton 322 (Babylonian mathematics c. 1900 BC), the Rhind Mathematical Papyrus (Egyptian mathematics c. 2000-1800 BC) and the Moscow Mathematical Papyrus (Egyptian mathematics c. 1890 BC). All of these texts concern the so-called Pythagorean theorem, which seems to be the most ancient and widespread mathematical development after basic arithmetic and geometry.
The study of mathematics as a subject in its own right begins in the 6th century BC with the Pythagoreans, who coined the term "mathematics" from the ancient Greekμάθημα (mathema), meaning "subject of instruction". Greek mathematics greatly refined the methods (especially through the introduction of deductive reasoning and mathematical rigor in proofs) and expanded the subject matter of mathematics. Chinese mathematics made early contributions, including a place value system. The Hindu-Arabic numeral system and the rules for the use of its operations, in use throughout the world today, likely evolved over the course of the first millennium AD in India and was transmitted to the west via Islamic mathematics. Islamic mathematics, in turn, developed and expanded the mathematics known to these civilizations. Many Greek and Arabic texts on mathematics were then translated into Latin, which led to further development of mathematics in medieval Europe.
From ancient times through the Middle Ages, bursts of mathematical creativity were often followed by centuries of stagnation. Beginning in Renaissance Italy in the 16th century, new mathematical developments, interacting with new scientific discoveries, were made at an increasing pace that continues through the present day.
Prehistoric Mathematics
The origin of mathematical thought lie in the concepts of number, magnitude, and form. Modern studies of animal cognition have shown that these concepts are not unique to humans. Such concepts would have been part of everyday life in hunter-gatherer societies. The idea of the "number" concept evolving gradually over time is supported by the existence of languages which preserve the distinction between "one", "two", and "many", but not of numbers larger than two.
The oldest known possibly mathematical object is the Lebombo bone, discovered in the Lebombo mountains of Swaziland and dated to approximately 35,000 BC. It consists of 29 distinct notches cut into a baboon's fibula.Also prehistoric artifacts discovered in Africa and France, dated between 35,000 and 20,000 years old, suggest early attempts to quantify time.
The Ishango bone, found near the headwaters of the Nile river (northeastern Congo), may be as much as 20,000 years old and consists of a series of tally marks carved in three columns running the length of the bone. Common interpretations are that the Ishango bone shows either the earliest known demonstration of sequences of prime numbers or a six-month lunar calendar. In the book How Mathematics Happened: The First 50,000 Years, Peter Rudman argues that the development of the concept of prime numbers could only have come about after the concept of division, which he dates to after 10,000 BC, with prime numbers probably not being understood until about 500 BC. He also writes that "no attempt has been made to explain why a tally of something should exhibit multiples of two, prime numbers between 10 and 20, and some numbers that are almost multiples of 10." The Ishango bone, according to scholar Alexander Marshack, may have influenced the later development of mathematics in Egypt as, like some entries on the Ishango bone, Egyptian arithmetic also made use of multiplication by 2; this, however, is disputed.
Predynastic Egyptians of the 5th millennium BC pictorially represented geometric designs. It has been claimed that megalithicmonuments in England and Scotland, dating from the 3rd millennium BC, incorporate geometric ideas such as circles, ellipses, andPythagorean triples in their design.
All of the above are disputed however, and the currently oldest undisputed mathematical usage is in Babylonian and dynastic Egyptian sources. Thus it took human beings at least 45,000 years from the attainment of behavioral modernity and language (generally thought to be a long time before that) to develop mathematics as such.
The origin of mathematical thought lie in the concepts of number, magnitude, and form. Modern studies of animal cognition have shown that these concepts are not unique to humans. Such concepts would have been part of everyday life in hunter-gatherer societies. The idea of the "number" concept evolving gradually over time is supported by the existence of languages which preserve the distinction between "one", "two", and "many", but not of numbers larger than two.
The oldest known possibly mathematical object is the Lebombo bone, discovered in the Lebombo mountains of Swaziland and dated to approximately 35,000 BC. It consists of 29 distinct notches cut into a baboon's fibula.Also prehistoric artifacts discovered in Africa and France, dated between 35,000 and 20,000 years old, suggest early attempts to quantify time.
The Ishango bone, found near the headwaters of the Nile river (northeastern Congo), may be as much as 20,000 years old and consists of a series of tally marks carved in three columns running the length of the bone. Common interpretations are that the Ishango bone shows either the earliest known demonstration of sequences of prime numbers or a six-month lunar calendar. In the book How Mathematics Happened: The First 50,000 Years, Peter Rudman argues that the development of the concept of prime numbers could only have come about after the concept of division, which he dates to after 10,000 BC, with prime numbers probably not being understood until about 500 BC. He also writes that "no attempt has been made to explain why a tally of something should exhibit multiples of two, prime numbers between 10 and 20, and some numbers that are almost multiples of 10." The Ishango bone, according to scholar Alexander Marshack, may have influenced the later development of mathematics in Egypt as, like some entries on the Ishango bone, Egyptian arithmetic also made use of multiplication by 2; this, however, is disputed.
Predynastic Egyptians of the 5th millennium BC pictorially represented geometric designs. It has been claimed that megalithicmonuments in England and Scotland, dating from the 3rd millennium BC, incorporate geometric ideas such as circles, ellipses, andPythagorean triples in their design.
All of the above are disputed however, and the currently oldest undisputed mathematical usage is in Babylonian and dynastic Egyptian sources. Thus it took human beings at least 45,000 years from the attainment of behavioral modernity and language (generally thought to be a long time before that) to develop mathematics as such.

Babylonian Mathematics
The Babylonian mathematical tablet Plimpton 322, dated to 1800 BC.
Babylonian mathematics refers to any mathematics of the people of Mesopotamia(modern Iraq) from the days of the early Sumerians through the Hellenistic periodalmost to the dawn of Christianity. It is named Babylonian mathematics due to the central role of Babylon as a place of study. Later under the Arab Empire, Mesopotamia, especially Baghdad, once again became an important center of study for Islamic mathematics.
In contrast to the sparsity of sources in Egyptian mathematics, our knowledge of Babylonian mathematics is derived from more than 400 clay tablets unearthed since the 1850s. Written in Cuneiform script, tablets were inscribed whilst the clay was moist, and baked hard in an oven or by the heat of the sun. Some of these appear to be graded homework.
The earliest evidence of written mathematics dates back to the ancient Sumerians, who built the earliest civilization in Mesopotamia. They developed a complex system of metrology from 3000 BC. From around 2500 BC onward, the Sumerians wrote multiplication tables on clay tablets and dealt with geometrical exercises and division problems. The earliest traces of the Babylonian numerals also date back to this period.
The majority of recovered clay tablets date from 1800 to 1600 BC, and cover topics which include fractions, algebra, quadratic and cubic equations, and the calculation of regular reciprocal pairs. The tablets also include multiplication tables and methods for solving linearand quadratic equations. The Babylonian tablet YBC 7289 gives an approximation of √2 accurate to five decimal places.
Babylonian mathematics were written using a sexagesimal (base-60) numeral system. From this derives the modern day usage of 60 seconds in a minute, 60 minutes in an hour, and 360 (60 x 6) degrees in a circle, as well as the use of seconds and minutes of arc to denote fractions of a degree. Babylonian advances in mathematics were facilitated by the fact that 60 has many divisors. Also, unlike the Egyptians, Greeks, and Romans, the Babylonians had a true place-value system, where digits written in the left column represented larger values, much as in the decimal system. They lacked, however, an equivalent of the decimal point, and so the place value of a symbol often had to be inferred from the context. On the other hand, this "defect" is equivalent to the modern-day usage of floating point arithmetic; moreover, the use of base 60 means that any reciprocal of an integer which is a multiple of divisors of 60 necessarily has a finite expansion to the base 60. (In decimal arithmetic, only reciprocals of multiples of 2 and 5 have finite decimal expansions.) Accordingly, there is a strong argument that arithmetic Old Babylonian style is considerably more sophisticated than that of current usage.
The interpretation of Plimpton 322 was the source of controversy for many years after its significance in the context of Pythagorean triangles was realized. In historical context, inheritance problems involving equal-area subdivision of triangular and trapezoidal fields (with integer length sides) quickly convert into the need to calculate the square root of 2, or to solve the "Pythagorean equation" in integers.
Rather than considering a square as the sum of two squares, we can equivalently consider a square as a difference of two squares. Let a, b and c be integers that form a Pythagorean Triple: a^2 + b^2 = c^2. Then c^2 - a^2 = b^2, and using the expansion for the difference of two squares we get (c-a)(c+a)= b^2. Dividing by b^2, it becomes the product of two rational numbers giving 1: (c/b - a/b)(c/b + a/b) = 1. We require two rational numbers which are reciprocals and which differ by 2(a/b). This is easily solved by consulting a table of reciprocal pairs. E.g., (1/2) (2) = 1 is a pair of reciprocals which differ by 3/2 = 2(a/b) Thus a/b = 3/4, giving a=3, b=4 and so c=5.
Solutions of the original equation are thus constructed by choosing a rational number x, from which Pythagorean-triples are 2x, x^2-1, x^2+1. Other triples are made by scaling these by an integer (the scaling integer being half the difference between the largest and one other side). All Pythagorean triples arise in this way, and the examples provided in Plimpton 322 involve some quite large numbers, by modern standards, such as (4601, 4800, 6649) in decimal notation.
The Babylonian mathematical tablet Plimpton 322, dated to 1800 BC.
Babylonian mathematics refers to any mathematics of the people of Mesopotamia(modern Iraq) from the days of the early Sumerians through the Hellenistic periodalmost to the dawn of Christianity. It is named Babylonian mathematics due to the central role of Babylon as a place of study. Later under the Arab Empire, Mesopotamia, especially Baghdad, once again became an important center of study for Islamic mathematics.
In contrast to the sparsity of sources in Egyptian mathematics, our knowledge of Babylonian mathematics is derived from more than 400 clay tablets unearthed since the 1850s. Written in Cuneiform script, tablets were inscribed whilst the clay was moist, and baked hard in an oven or by the heat of the sun. Some of these appear to be graded homework.
The earliest evidence of written mathematics dates back to the ancient Sumerians, who built the earliest civilization in Mesopotamia. They developed a complex system of metrology from 3000 BC. From around 2500 BC onward, the Sumerians wrote multiplication tables on clay tablets and dealt with geometrical exercises and division problems. The earliest traces of the Babylonian numerals also date back to this period.
The majority of recovered clay tablets date from 1800 to 1600 BC, and cover topics which include fractions, algebra, quadratic and cubic equations, and the calculation of regular reciprocal pairs. The tablets also include multiplication tables and methods for solving linearand quadratic equations. The Babylonian tablet YBC 7289 gives an approximation of √2 accurate to five decimal places.
Babylonian mathematics were written using a sexagesimal (base-60) numeral system. From this derives the modern day usage of 60 seconds in a minute, 60 minutes in an hour, and 360 (60 x 6) degrees in a circle, as well as the use of seconds and minutes of arc to denote fractions of a degree. Babylonian advances in mathematics were facilitated by the fact that 60 has many divisors. Also, unlike the Egyptians, Greeks, and Romans, the Babylonians had a true place-value system, where digits written in the left column represented larger values, much as in the decimal system. They lacked, however, an equivalent of the decimal point, and so the place value of a symbol often had to be inferred from the context. On the other hand, this "defect" is equivalent to the modern-day usage of floating point arithmetic; moreover, the use of base 60 means that any reciprocal of an integer which is a multiple of divisors of 60 necessarily has a finite expansion to the base 60. (In decimal arithmetic, only reciprocals of multiples of 2 and 5 have finite decimal expansions.) Accordingly, there is a strong argument that arithmetic Old Babylonian style is considerably more sophisticated than that of current usage.
The interpretation of Plimpton 322 was the source of controversy for many years after its significance in the context of Pythagorean triangles was realized. In historical context, inheritance problems involving equal-area subdivision of triangular and trapezoidal fields (with integer length sides) quickly convert into the need to calculate the square root of 2, or to solve the "Pythagorean equation" in integers.
Rather than considering a square as the sum of two squares, we can equivalently consider a square as a difference of two squares. Let a, b and c be integers that form a Pythagorean Triple: a^2 + b^2 = c^2. Then c^2 - a^2 = b^2, and using the expansion for the difference of two squares we get (c-a)(c+a)= b^2. Dividing by b^2, it becomes the product of two rational numbers giving 1: (c/b - a/b)(c/b + a/b) = 1. We require two rational numbers which are reciprocals and which differ by 2(a/b). This is easily solved by consulting a table of reciprocal pairs. E.g., (1/2) (2) = 1 is a pair of reciprocals which differ by 3/2 = 2(a/b) Thus a/b = 3/4, giving a=3, b=4 and so c=5.
Solutions of the original equation are thus constructed by choosing a rational number x, from which Pythagorean-triples are 2x, x^2-1, x^2+1. Other triples are made by scaling these by an integer (the scaling integer being half the difference between the largest and one other side). All Pythagorean triples arise in this way, and the examples provided in Plimpton 322 involve some quite large numbers, by modern standards, such as (4601, 4800, 6649) in decimal notation.

Egyptian mathematics
Image of Problem 14 from the Moscow Mathematical Papyrus. The problem includes a diagram indicating the dimensions of the truncated pyramid.
Egyptian mathematics refers to mathematics written in the Egyptian language. From the Hellenistic period, Greek replaced Egyptian as the written language of Egyptian scholars. Mathematical study in Egypt later continued under theArab Empire as part of Islamic mathematics, when Arabic became the written language of Egyptian scholars.
The most extensive Egyptian mathematical text is the Rhind papyrus(sometimes also called the Ahmes Papyrus after its author), dated to c. 1650 BC but likely a copy of an older document from the Middle Kingdom of about 2000-1800 BC. It is an instruction manual for students in arithmetic and geometry. In addition to giving area formulas and methods for multiplication, division and working with unit fractions, it also contains evidence of other mathematical knowledge, including composite and prime numbers;arithmetic, geometric and harmonic means; and simplistic understandings of both the Sieve of Eratosthenes and perfect number theory(namely, that of the number 6). It also shows how to solve first order linear equations as well as arithmetic and geometric series.
Another significant Egyptian mathematical text is the Moscow papyrus, also from the Middle Kingdom period, dated to c. 1890 BC. It consists of what are today called word problems or story problems, which were apparently intended as entertainment. One problem is considered to be of particular importance because it gives a method for finding the volume of a frustum: "If you are told: A truncated pyramid of 6 for the vertical height by 4 on the base by 2 on the top. You are to square this 4, result 16. You are to double 4, result 8. You are to square 2, result 4. You are to add the 16, the 8, and the 4, result 28. You are to take one third of 6, result 2. You are to take 28 twice, result 56. See, it is 56. You will find it right."
Finally, the Berlin Papyrus 6619 (c. 1800 BC) shows that ancient Egyptians could solve a second-order algebraic equation.
Image of Problem 14 from the Moscow Mathematical Papyrus. The problem includes a diagram indicating the dimensions of the truncated pyramid.
Egyptian mathematics refers to mathematics written in the Egyptian language. From the Hellenistic period, Greek replaced Egyptian as the written language of Egyptian scholars. Mathematical study in Egypt later continued under theArab Empire as part of Islamic mathematics, when Arabic became the written language of Egyptian scholars.
The most extensive Egyptian mathematical text is the Rhind papyrus(sometimes also called the Ahmes Papyrus after its author), dated to c. 1650 BC but likely a copy of an older document from the Middle Kingdom of about 2000-1800 BC. It is an instruction manual for students in arithmetic and geometry. In addition to giving area formulas and methods for multiplication, division and working with unit fractions, it also contains evidence of other mathematical knowledge, including composite and prime numbers;arithmetic, geometric and harmonic means; and simplistic understandings of both the Sieve of Eratosthenes and perfect number theory(namely, that of the number 6). It also shows how to solve first order linear equations as well as arithmetic and geometric series.
Another significant Egyptian mathematical text is the Moscow papyrus, also from the Middle Kingdom period, dated to c. 1890 BC. It consists of what are today called word problems or story problems, which were apparently intended as entertainment. One problem is considered to be of particular importance because it gives a method for finding the volume of a frustum: "If you are told: A truncated pyramid of 6 for the vertical height by 4 on the base by 2 on the top. You are to square this 4, result 16. You are to double 4, result 8. You are to square 2, result 4. You are to add the 16, the 8, and the 4, result 28. You are to take one third of 6, result 2. You are to take 28 twice, result 56. See, it is 56. You will find it right."
Finally, the Berlin Papyrus 6619 (c. 1800 BC) shows that ancient Egyptians could solve a second-order algebraic equation.
Greek Mathematics
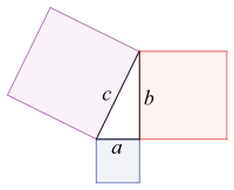
The Pythagorean theorem. The Pythagoreans are generally credited with the first proof of the theorem.
Greek mathematics refers to the mathematics written in the Greek language from the time of Thales of Miletus (~600 BC) to the closure of the Academy of Athens in 529 AD. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to North Africa, but were united by culture and language. Greek mathematics of the period following Alexander the Great is sometimes called Hellenistic mathematics.
Greek mathematics was much more sophisticated than the mathematics that had been developed by earlier cultures. All surviving records of pre-Greek mathematics show the use of inductive reasoning, that is, repeated observations used to establish rules of thumb. Greek mathematicians, by contrast, used deductive reasoning. The Greeks used logic to derive conclusions from definitions and axioms, and used mathematical rigor to prove them.
Greek mathematics is thought to have begun with Thales of Miletus (c. 624–c.546 BC) andPythagoras of Samos (c. 582–c. 507 BC). Although the extent of the influence is disputed, they were probably inspired by Egyptian and Babylonian mathematics. According to legend, Pythagoras traveled to Egypt to learn mathematics, geometry, and astronomy from Egyptian priests.
The Pythagorean theorem. The Pythagoreans are generally credited with the first proof of the theorem.
Greek mathematics refers to the mathematics written in the Greek language from the time of Thales of Miletus (~600 BC) to the closure of the Academy of Athens in 529 AD. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to North Africa, but were united by culture and language. Greek mathematics of the period following Alexander the Great is sometimes called Hellenistic mathematics.
Greek mathematics was much more sophisticated than the mathematics that had been developed by earlier cultures. All surviving records of pre-Greek mathematics show the use of inductive reasoning, that is, repeated observations used to establish rules of thumb. Greek mathematicians, by contrast, used deductive reasoning. The Greeks used logic to derive conclusions from definitions and axioms, and used mathematical rigor to prove them.
Greek mathematics is thought to have begun with Thales of Miletus (c. 624–c.546 BC) andPythagoras of Samos (c. 582–c. 507 BC). Although the extent of the influence is disputed, they were probably inspired by Egyptian and Babylonian mathematics. According to legend, Pythagoras traveled to Egypt to learn mathematics, geometry, and astronomy from Egyptian priests.
Chinese Mathematics
Early Chinese mathematics is so different from that of other parts of the world that it is reasonable to assume independent development. The oldest extant mathematical text from China is the Chou Pei Suan Ching, variously dated to between 1200 BC and 100 BC, though a date of about 300 BC appears reasonable.
Of particular note is the use in Chinese mathematics of a decimal positional notation system, the so-called "rod numerals" in which distinct ciphers were used for numbers between 1 and 10, and additional ciphers for powers of ten. Thus, the number 123 would be written using the symbol for "1", followed by the symbol for "100", then the symbol for "2" followed by the symbol for "10", followed by the symbol for "3". This was the most advanced number system in the world at the time, apparently in use several centuries before the common era and well before the development of the Indian numeral system. Rod numerals allowed the representation of numbers as large as desired and allowed calculations to be carried out on the suan pan, or Chinese abacus. The date of the invention of the suan pan is not certain, but the earliest written mention dates from AD 190, in Xu Yue's Supplementary Notes on the Art of Figures.
The oldest existent work on geometry in China comes from the philosophical Mohist canon c. 330 BC, compiled by the followers of Mozi (470–390 BC). The Mo Jing described various aspects of many fields associated with physical science, and provided a small number of geometrical theorems as well.
In 212 BC, the Emperor Qin Shi Huang (Shi Huang-ti) commanded all books in the Qin Empire other than officially sanctioned ones be burned. This decree was not universally obeyed, but as a consequence of this order little is known about ancient Chinese mathematics before this date. After the book burning of 212 BC, the Han dynasty (202 BC–220 AD) produced works of mathematics which presumably expanded on works that are now lost. The most important of these is The Nine Chapters on the Mathematical Art, the full title of which appeared by AD 179, but existed in part under other titles beforehand. It consists of 246 word problems involving agriculture, business, employment of geometry to figure height spans and dimension ratios for Chinese pagoda towers, engineering,surveying, and includes material on right triangles and values of π. It created mathematical proof for the Pythagorean theorem, and a mathematical formula for Gaussian elimination. Liu Hui commented on the work in the 3rd century AD, and gave a value of π accurate to 5 decimal places. Though more of a matter of computational stamina than theoretical insight, in the 5th century AD Zu Chongzhi computed the value of π to seven decimal places, which remained the most accurate value of π for almost the next 1000 years. He also established a method which would later be called Cavalieri's principle to find the volume of a sphere.
The high-water mark of Chinese mathematics occurs in the 13th century (latter part of the Sung period), with the development of Chinese algebra. The most important text from that period is the Precious Mirror of the Four Elements by Chu Shih-chieh (fl. 1280-1303), dealing with the solution of simultaneous higher order algebraic equations using a method similar to Horner's method. The Precious Mirror also contains a diagram of Pascal's triangle with coefficients of binomial expansions through the eighth power, though both appear in Chinese works as early as 1100. The Chinese also made use of the complex combination diagram known as the magic square and magic circles, described in ancient times and perfected by Yang Hui (AD 1238–1298).
Even after European mathematics began to flourish during the Renaissance, European and Chinese mathematics were separate traditions, with significant Chinese mathematical output in decline from the 13th century onwards. Jesuit missionaries such as Matteo Ricci carried mathematical ideas back and forth between the two cultures from the 16th to 18th centuries, though at this point far more mathematical ideas were entering China than leaving.
Early Chinese mathematics is so different from that of other parts of the world that it is reasonable to assume independent development. The oldest extant mathematical text from China is the Chou Pei Suan Ching, variously dated to between 1200 BC and 100 BC, though a date of about 300 BC appears reasonable.
Of particular note is the use in Chinese mathematics of a decimal positional notation system, the so-called "rod numerals" in which distinct ciphers were used for numbers between 1 and 10, and additional ciphers for powers of ten. Thus, the number 123 would be written using the symbol for "1", followed by the symbol for "100", then the symbol for "2" followed by the symbol for "10", followed by the symbol for "3". This was the most advanced number system in the world at the time, apparently in use several centuries before the common era and well before the development of the Indian numeral system. Rod numerals allowed the representation of numbers as large as desired and allowed calculations to be carried out on the suan pan, or Chinese abacus. The date of the invention of the suan pan is not certain, but the earliest written mention dates from AD 190, in Xu Yue's Supplementary Notes on the Art of Figures.
The oldest existent work on geometry in China comes from the philosophical Mohist canon c. 330 BC, compiled by the followers of Mozi (470–390 BC). The Mo Jing described various aspects of many fields associated with physical science, and provided a small number of geometrical theorems as well.
In 212 BC, the Emperor Qin Shi Huang (Shi Huang-ti) commanded all books in the Qin Empire other than officially sanctioned ones be burned. This decree was not universally obeyed, but as a consequence of this order little is known about ancient Chinese mathematics before this date. After the book burning of 212 BC, the Han dynasty (202 BC–220 AD) produced works of mathematics which presumably expanded on works that are now lost. The most important of these is The Nine Chapters on the Mathematical Art, the full title of which appeared by AD 179, but existed in part under other titles beforehand. It consists of 246 word problems involving agriculture, business, employment of geometry to figure height spans and dimension ratios for Chinese pagoda towers, engineering,surveying, and includes material on right triangles and values of π. It created mathematical proof for the Pythagorean theorem, and a mathematical formula for Gaussian elimination. Liu Hui commented on the work in the 3rd century AD, and gave a value of π accurate to 5 decimal places. Though more of a matter of computational stamina than theoretical insight, in the 5th century AD Zu Chongzhi computed the value of π to seven decimal places, which remained the most accurate value of π for almost the next 1000 years. He also established a method which would later be called Cavalieri's principle to find the volume of a sphere.
The high-water mark of Chinese mathematics occurs in the 13th century (latter part of the Sung period), with the development of Chinese algebra. The most important text from that period is the Precious Mirror of the Four Elements by Chu Shih-chieh (fl. 1280-1303), dealing with the solution of simultaneous higher order algebraic equations using a method similar to Horner's method. The Precious Mirror also contains a diagram of Pascal's triangle with coefficients of binomial expansions through the eighth power, though both appear in Chinese works as early as 1100. The Chinese also made use of the complex combination diagram known as the magic square and magic circles, described in ancient times and perfected by Yang Hui (AD 1238–1298).
Even after European mathematics began to flourish during the Renaissance, European and Chinese mathematics were separate traditions, with significant Chinese mathematical output in decline from the 13th century onwards. Jesuit missionaries such as Matteo Ricci carried mathematical ideas back and forth between the two cultures from the 16th to 18th centuries, though at this point far more mathematical ideas were entering China than leaving.
Indian Mathematics
The numerals used in the Bakhshali manuscript, dated between the 2nd century BCE and the 2nd century BCE. The earliest civilization on the Indian subcontinent is the Indus Valley Civilization that flourished between 2600 and 1900 BC in the Indus river basin. Their cities were laid out with geometric regularity, but no known mathematical documents survive from this civilization.
The oldest extant mathematical records from India are the Sulba Sutras (dated variously between the 8th century BC and the 2nd century AD), appendices to religious texts which give simple rules for constructing altars of various shapes, such as squares, rectangles, parallelograms, and others. As with Egypt, the preoccupation with temple functions points to an origin of mathematics in religious ritual. The Sulba Sutras give methods for constructing a circle with approximately the same area as a given square, which imply several different approximations of the value of π. In addition, they compute the square root of 2 to several decimal places, list Pythagorean triples, and give a statement of the Pythagorean theorem. All of these results are present in Babylonian mathematics, indicating Mesopotamian influence. It is not known to what extent the Sulba Sutras influenced later Indian mathematicians. As in China, there is a lack of continuity in Indian mathematics; significant advances are separated by long periods of inactivity.
Pāṇini (c. 5th century BC) formulated the rules for Sanskrit grammar. His notation was similar to modern mathematical notation, and used metarules, transformations, and recursion Pingala (roughly 3rd-1st centuries BC) in his treatise of prosody uses a device corresponding to a binary numeral system. His discussion of the combinatorics of meters corresponds to an elementary version of the binomial theorem. Pingala's work also contains the basic ideas of Fibonacci numbers (called mātrāmeru).
The next significant mathematical documents from India after the Sulba Sutras are the Siddhantas, astronomical treatises from the 4th and 5th centuries AD (Gupta period) showing strong Hellenistic influence. They are significant in that they contain the first instance of trigonometric relations based on the half-chord, as is the case in modern trigonometry, rather than the full chord, as was the case in Ptolemaic trigonometry. Through a series of translation errors, the words "sine" and "cosine" derive from the Sanskrit "jiya" and "kojiya".
In the 5th century AD, Aryabhata wrote the Aryabhatiya, a slim volume, written in verse, intended to supplement the rules of calculation used in astronomy and mathematical mensuration, though with no feeling for logic or deductive methodology. Though about half of the entries are wrong, it is in the Aryabhatiya that the decimal place-value system first appears. Several centuries later, the Muslim mathematician Abu Rayhan Biruni described the Aryabhatiya as a "mix of common pebbles and costly crystals".
In the 7th century, Brahmagupta identified the Brahmagupta theorem, Brahmagupta's identity and Brahmagupta's formula, and for the first time, in Brahma-sphuta-siddhanta, he lucidly explained the use of zero as both a placeholder and decimal digit, and explained the Hindu-Arabic numeral system. It was from a translation of this Indian text on mathematics (c. 770) that Islamic mathematicians were introduced to this numeral system, which they adapted as Arabic numerals. Islamic scholars carried knowledge of this number system to Europe by the 12th century, and it has now displaced all older number systems throughout the world. In the 10th century,Halayudha's commentary on Pingala's work contains a study of the Fibonacci sequence and Pascal's triangle, and describes the formation of a matrix.
In the 12th century, Bhāskara Iived in southern India and wrote extensively on all then known branches of mathematics. His work contains mathematical objects equivalent or approximately equivalent to infinitesimals, derivatives, the mean value theorem and the derivative of the sine function. To what extent he anticipated the invention of calculus is a controversial subject among historians of mathematics.
The numerals used in the Bakhshali manuscript, dated between the 2nd century BCE and the 2nd century BCE. The earliest civilization on the Indian subcontinent is the Indus Valley Civilization that flourished between 2600 and 1900 BC in the Indus river basin. Their cities were laid out with geometric regularity, but no known mathematical documents survive from this civilization.
The oldest extant mathematical records from India are the Sulba Sutras (dated variously between the 8th century BC and the 2nd century AD), appendices to religious texts which give simple rules for constructing altars of various shapes, such as squares, rectangles, parallelograms, and others. As with Egypt, the preoccupation with temple functions points to an origin of mathematics in religious ritual. The Sulba Sutras give methods for constructing a circle with approximately the same area as a given square, which imply several different approximations of the value of π. In addition, they compute the square root of 2 to several decimal places, list Pythagorean triples, and give a statement of the Pythagorean theorem. All of these results are present in Babylonian mathematics, indicating Mesopotamian influence. It is not known to what extent the Sulba Sutras influenced later Indian mathematicians. As in China, there is a lack of continuity in Indian mathematics; significant advances are separated by long periods of inactivity.
Pāṇini (c. 5th century BC) formulated the rules for Sanskrit grammar. His notation was similar to modern mathematical notation, and used metarules, transformations, and recursion Pingala (roughly 3rd-1st centuries BC) in his treatise of prosody uses a device corresponding to a binary numeral system. His discussion of the combinatorics of meters corresponds to an elementary version of the binomial theorem. Pingala's work also contains the basic ideas of Fibonacci numbers (called mātrāmeru).
The next significant mathematical documents from India after the Sulba Sutras are the Siddhantas, astronomical treatises from the 4th and 5th centuries AD (Gupta period) showing strong Hellenistic influence. They are significant in that they contain the first instance of trigonometric relations based on the half-chord, as is the case in modern trigonometry, rather than the full chord, as was the case in Ptolemaic trigonometry. Through a series of translation errors, the words "sine" and "cosine" derive from the Sanskrit "jiya" and "kojiya".
In the 5th century AD, Aryabhata wrote the Aryabhatiya, a slim volume, written in verse, intended to supplement the rules of calculation used in astronomy and mathematical mensuration, though with no feeling for logic or deductive methodology. Though about half of the entries are wrong, it is in the Aryabhatiya that the decimal place-value system first appears. Several centuries later, the Muslim mathematician Abu Rayhan Biruni described the Aryabhatiya as a "mix of common pebbles and costly crystals".
In the 7th century, Brahmagupta identified the Brahmagupta theorem, Brahmagupta's identity and Brahmagupta's formula, and for the first time, in Brahma-sphuta-siddhanta, he lucidly explained the use of zero as both a placeholder and decimal digit, and explained the Hindu-Arabic numeral system. It was from a translation of this Indian text on mathematics (c. 770) that Islamic mathematicians were introduced to this numeral system, which they adapted as Arabic numerals. Islamic scholars carried knowledge of this number system to Europe by the 12th century, and it has now displaced all older number systems throughout the world. In the 10th century,Halayudha's commentary on Pingala's work contains a study of the Fibonacci sequence and Pascal's triangle, and describes the formation of a matrix.
In the 12th century, Bhāskara Iived in southern India and wrote extensively on all then known branches of mathematics. His work contains mathematical objects equivalent or approximately equivalent to infinitesimals, derivatives, the mean value theorem and the derivative of the sine function. To what extent he anticipated the invention of calculus is a controversial subject among historians of mathematics.

Islamic Mathematics
Page from The Compendious Book on Calculation by Completion and Balancingby Muhammad ibn Mūsā al-Khwārizmī (c. AD 820)
The Islamic Empire established across Persia, the Middle East, Central Asia, North Africa,Iberia, and in parts of India in the 8th century made significant contributions towards mathematics. Although most Islamic texts on mathematics were written in Arabic, most of them were not written by Arabs, since much like the status of Greek in the Hellenistic world, Arabic was used as the written language of non-Arab scholars throughout the Islamic world at the time. Persians contributed to the world of Mathematics alongside Arabs.
In the 9th century, the Persian mathematician Muḥammad ibn Mūsā al-Khwārizmī wrote several important books on the Hindu-Arabic numerals and on methods for solving equations. His book On the Calculation with Hindu Numerals, written about 825, along with the work of Al-Kindi, were instrumental in spreading Indian mathematics and Indian numerals to the West. The word algorithm is derived from the Latinization of his name, Algoritmi, and the word algebra from the title of one of his works, Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala (The Compendious Book on Calculation by Completion and Balancing). He gave an exhaustive explanation for the algebraic solution of quadratic equations with positive roots, and he was the first to teach algebra in an elementary form and for its own sake. He also discussed the fundamental method of "reduction" and "balancing", referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation. This is the operation which al-Khwārizmī originally described as al-jabr. His algebra was also no longer concerned "with a series of problems to be resolved, but an exposition which starts with primitive terms in which the combinations must give all possible prototypes for equations, which henceforward explicitly constitute the true object of study." He also studied an equation for its own sake and "in a generic manner, insofar as it does not simply emerge in the course of solving a problem, but is specifically called on to define an infinite class of problems."
Page from The Compendious Book on Calculation by Completion and Balancingby Muhammad ibn Mūsā al-Khwārizmī (c. AD 820)
The Islamic Empire established across Persia, the Middle East, Central Asia, North Africa,Iberia, and in parts of India in the 8th century made significant contributions towards mathematics. Although most Islamic texts on mathematics were written in Arabic, most of them were not written by Arabs, since much like the status of Greek in the Hellenistic world, Arabic was used as the written language of non-Arab scholars throughout the Islamic world at the time. Persians contributed to the world of Mathematics alongside Arabs.
In the 9th century, the Persian mathematician Muḥammad ibn Mūsā al-Khwārizmī wrote several important books on the Hindu-Arabic numerals and on methods for solving equations. His book On the Calculation with Hindu Numerals, written about 825, along with the work of Al-Kindi, were instrumental in spreading Indian mathematics and Indian numerals to the West. The word algorithm is derived from the Latinization of his name, Algoritmi, and the word algebra from the title of one of his works, Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala (The Compendious Book on Calculation by Completion and Balancing). He gave an exhaustive explanation for the algebraic solution of quadratic equations with positive roots, and he was the first to teach algebra in an elementary form and for its own sake. He also discussed the fundamental method of "reduction" and "balancing", referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation. This is the operation which al-Khwārizmī originally described as al-jabr. His algebra was also no longer concerned "with a series of problems to be resolved, but an exposition which starts with primitive terms in which the combinations must give all possible prototypes for equations, which henceforward explicitly constitute the true object of study." He also studied an equation for its own sake and "in a generic manner, insofar as it does not simply emerge in the course of solving a problem, but is specifically called on to define an infinite class of problems."
Medieval European Mathematics
Medieval European interest in mathematics was driven by concerns quite different from those of modern mathematicians. One driving element was the belief that mathematics provided the key to understanding the created order of nature, frequently justified by Plato'sTimaeus and the biblical passage (in the Book of Wisdom) that God had ordered all things in measure, and number, and weight.
Boethius provided a place for mathematics in the curriculum in the 6th century when he coined the term quadrivium to describe the study of arithmetic, geometry, astronomy, and music. He wrote De institutione arithmetica, a free translation from the Greek of Nicomachus's Introduction to Arithmetic; De institutione musica, also derived from Greek sources; and a series of excerpts from Euclid's Elements. His works were theoretical, rather than practical, and were the basis of mathematical study until the recovery of Greek and Arabic mathematical works.
In the 12th century, European scholars traveled to Spain and Sicily seeking scientific Arabic texts, including al-Khwārizmī's The Compendious Book on Calculation by Completion and Balancing, translated into Latin by Robert of Chester, and the complete text ofEuclid's Elements, translated in various versions by Adelard of Bath, Herman of Carinthia, and Gerard of Cremona.
Medieval European interest in mathematics was driven by concerns quite different from those of modern mathematicians. One driving element was the belief that mathematics provided the key to understanding the created order of nature, frequently justified by Plato'sTimaeus and the biblical passage (in the Book of Wisdom) that God had ordered all things in measure, and number, and weight.
Boethius provided a place for mathematics in the curriculum in the 6th century when he coined the term quadrivium to describe the study of arithmetic, geometry, astronomy, and music. He wrote De institutione arithmetica, a free translation from the Greek of Nicomachus's Introduction to Arithmetic; De institutione musica, also derived from Greek sources; and a series of excerpts from Euclid's Elements. His works were theoretical, rather than practical, and were the basis of mathematical study until the recovery of Greek and Arabic mathematical works.
In the 12th century, European scholars traveled to Spain and Sicily seeking scientific Arabic texts, including al-Khwārizmī's The Compendious Book on Calculation by Completion and Balancing, translated into Latin by Robert of Chester, and the complete text ofEuclid's Elements, translated in various versions by Adelard of Bath, Herman of Carinthia, and Gerard of Cremona.

Renaissance Mathematics
Portrait of Luca Pacioli, a painting traditionally attributed to Jacopo de' Barbari, 1495, (Museo di Capodimonte).
During the Renaissance, the development of mathematics and of accounting were intertwined. While there is no direct relationship between algebra and accounting, the teaching of the subjects and the books published often intended for the children of merchants who were sent to reckoning schools (in Flanders and Germany) or abacus schools (known as abbaco in Italy), where they learned the skills useful for trade and commerce. There is probably no need for algebra in performing bookkeeping operations, but for complex bartering operations or the calculation of compound interest, a basic knowledge of arithmetic was mandatory and knowledge of algebra was very useful.
Luca Pacioli's "Summa de Arithmetica, Geometria, Proportioni et Proportionalità"(Italian: "Review of Arithmetic, Geometry, Ratio and Proportion") was first printed and published in Venice in 1494. It included a 27-page treatise on bookkeeping,"Particularis de Computis et Scripturis" (Italian: "Details of Calculation and Recording"). It was written primarily for, and sold mainly to, merchants who used the book as a reference text, as a source of pleasure from the mathematical puzzles it contained, and to aid the education of their sons. In Summa Arithmetica, Pacioli introduced symbols for plus and minus for the first time in a printed book, symbols that became standard notation in Italian Renaissance mathematics. Summa Arithmetica was also the first known book printed in Italy to contain algebra. It is important to note that Pacioli himself had borrowed much of the work of Piero Della Francesca whom he plagiarized.
In Italy, during the first half of the 16th century, Scipione del Ferro and Niccolò Fontana Tartaglia discovered solutions for cubic equations. Gerolamo Cardano published them in his 1545 book Ars Magna, together with a solution for the quartic equations, discovered by his student Lodovico Ferrari. In 1572 Rafael Bombelli published his L'Algebra in which he showed how to deal with the imaginary quantities that could appear in Cardano's formula for solving cubic equations.
Portrait of Luca Pacioli, a painting traditionally attributed to Jacopo de' Barbari, 1495, (Museo di Capodimonte).
During the Renaissance, the development of mathematics and of accounting were intertwined. While there is no direct relationship between algebra and accounting, the teaching of the subjects and the books published often intended for the children of merchants who were sent to reckoning schools (in Flanders and Germany) or abacus schools (known as abbaco in Italy), where they learned the skills useful for trade and commerce. There is probably no need for algebra in performing bookkeeping operations, but for complex bartering operations or the calculation of compound interest, a basic knowledge of arithmetic was mandatory and knowledge of algebra was very useful.
Luca Pacioli's "Summa de Arithmetica, Geometria, Proportioni et Proportionalità"(Italian: "Review of Arithmetic, Geometry, Ratio and Proportion") was first printed and published in Venice in 1494. It included a 27-page treatise on bookkeeping,"Particularis de Computis et Scripturis" (Italian: "Details of Calculation and Recording"). It was written primarily for, and sold mainly to, merchants who used the book as a reference text, as a source of pleasure from the mathematical puzzles it contained, and to aid the education of their sons. In Summa Arithmetica, Pacioli introduced symbols for plus and minus for the first time in a printed book, symbols that became standard notation in Italian Renaissance mathematics. Summa Arithmetica was also the first known book printed in Italy to contain algebra. It is important to note that Pacioli himself had borrowed much of the work of Piero Della Francesca whom he plagiarized.
In Italy, during the first half of the 16th century, Scipione del Ferro and Niccolò Fontana Tartaglia discovered solutions for cubic equations. Gerolamo Cardano published them in his 1545 book Ars Magna, together with a solution for the quartic equations, discovered by his student Lodovico Ferrari. In 1572 Rafael Bombelli published his L'Algebra in which he showed how to deal with the imaginary quantities that could appear in Cardano's formula for solving cubic equations.

Mathematics during the Scientific Revolution
Gottfried Wilhelm Leibniz.
The 17th century saw an unprecedented explosion of mathematical and scientific ideas across Europe.Galileo observed the moons of Jupiter in orbit about that planet, using a telescope based on a toy imported from Holland. Tycho Brahe had gathered an enormous quantity of mathematical data describing the positions of the planets in the sky. Through his position as Brahe's assistant, Johannes Kepler was first exposed to and seriously interacted with the topic of planetary motion. Kepler's calculations were made simpler by the contemporaneous invention of logarithms by John Napier and Jost Bürgi. Kepler succeeded in formulating mathematical laws of planetary motion. The analytic geometry developed by René Descartes (1596–1650) allowed those orbits to be plotted on a graph, in Cartesian coordinates.Simon Stevin (1585) created the basis for modern decimal notation capable of describing all numbers, whether rational or irrational.
Building on earlier work by many predecessors, Isaac Newton discovered the laws of physics explainingKepler's Laws, and brought together the concepts now known as infinitesimal calculus. Independently, Gottfried Wilhelm Leibniz, who is arguably one of the most important mathematicians of the 17th century, developed calculus and much of the calculus notation still in use today. Science and mathematics had become an international endeavor, which would soon spread over the entire world.
In addition to the application of mathematics to the studies of the heavens, applied mathematics began to expand into new areas, with the correspondence of Pierre de Fermat and Blaise Pascal. Pascal and Fermat set the groundwork for the investigations of probability theory and the corresponding rules of combinatorics in their discussions over a game of gambling. Pascal, with his wager, attempted to use the newly developing probability theory to argue for a life devoted to religion, on the grounds that even if the probability of success was small, the rewards were infinite. In some sense, this foreshadowed the development of utility theory in the 18th–19th century.
Gottfried Wilhelm Leibniz.
The 17th century saw an unprecedented explosion of mathematical and scientific ideas across Europe.Galileo observed the moons of Jupiter in orbit about that planet, using a telescope based on a toy imported from Holland. Tycho Brahe had gathered an enormous quantity of mathematical data describing the positions of the planets in the sky. Through his position as Brahe's assistant, Johannes Kepler was first exposed to and seriously interacted with the topic of planetary motion. Kepler's calculations were made simpler by the contemporaneous invention of logarithms by John Napier and Jost Bürgi. Kepler succeeded in formulating mathematical laws of planetary motion. The analytic geometry developed by René Descartes (1596–1650) allowed those orbits to be plotted on a graph, in Cartesian coordinates.Simon Stevin (1585) created the basis for modern decimal notation capable of describing all numbers, whether rational or irrational.
Building on earlier work by many predecessors, Isaac Newton discovered the laws of physics explainingKepler's Laws, and brought together the concepts now known as infinitesimal calculus. Independently, Gottfried Wilhelm Leibniz, who is arguably one of the most important mathematicians of the 17th century, developed calculus and much of the calculus notation still in use today. Science and mathematics had become an international endeavor, which would soon spread over the entire world.
In addition to the application of mathematics to the studies of the heavens, applied mathematics began to expand into new areas, with the correspondence of Pierre de Fermat and Blaise Pascal. Pascal and Fermat set the groundwork for the investigations of probability theory and the corresponding rules of combinatorics in their discussions over a game of gambling. Pascal, with his wager, attempted to use the newly developing probability theory to argue for a life devoted to religion, on the grounds that even if the probability of success was small, the rewards were infinite. In some sense, this foreshadowed the development of utility theory in the 18th–19th century.

18th Century
Leonhard Euler by Emanuel Handmann.
The most influential mathematician of the 18th century was arguably Leonhard Euler. His contributions range from founding the study of graph theory with the Seven Bridges of Königsberg problem to standardizing many modern mathematical terms and notations. For example, he named the square root of minus 1 with the symbol i, and he popularized the use of the Greek letter to stand for the ratio of a circle's circumference to its diameter. He made numerous contributions to the study of topology, graph theory, calculus, combinatorics, and complex analysis, as evidenced by the multitude of theorems and notations named for him.
Other important European mathematicians of the 18th century included Joseph Louis Lagrange, who did pioneering work in number theory, algebra, differential calculus, and the calculus of variations, and Laplace who, in the age of Napoleon, did important work on the foundations of celestial mechanics and on statistics.
Leonhard Euler by Emanuel Handmann.
The most influential mathematician of the 18th century was arguably Leonhard Euler. His contributions range from founding the study of graph theory with the Seven Bridges of Königsberg problem to standardizing many modern mathematical terms and notations. For example, he named the square root of minus 1 with the symbol i, and he popularized the use of the Greek letter to stand for the ratio of a circle's circumference to its diameter. He made numerous contributions to the study of topology, graph theory, calculus, combinatorics, and complex analysis, as evidenced by the multitude of theorems and notations named for him.
Other important European mathematicians of the 18th century included Joseph Louis Lagrange, who did pioneering work in number theory, algebra, differential calculus, and the calculus of variations, and Laplace who, in the age of Napoleon, did important work on the foundations of celestial mechanics and on statistics.
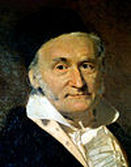
Modern Mathematics
Carl Friedrich Gauss.
Throughout the 19th century mathematics became increasingly abstract. In the 19th century lived Carl Friedrich Gauss (1777–1855). Leaving aside his many contributions to science, in pure mathematics he did revolutionary work on functions of complex variables, in geometry, and on the convergence of series. He gave the first satisfactory proofs of the fundamental theorem of algebra and of the quadratic reciprocity law.
Carl Friedrich Gauss.
Throughout the 19th century mathematics became increasingly abstract. In the 19th century lived Carl Friedrich Gauss (1777–1855). Leaving aside his many contributions to science, in pure mathematics he did revolutionary work on functions of complex variables, in geometry, and on the convergence of series. He gave the first satisfactory proofs of the fundamental theorem of algebra and of the quadratic reciprocity law.

20th century
A map illustrating the Four Color Theorem
The 20th century saw mathematics become a major profession. Every year, thousands of new Ph.D.s in mathematics were awarded, and jobs were available in both teaching and industry. An effort to catalogue the areas and applications of mathematics was undertaken in Klein's encyclopedia.
In a 1900 speech to the International Congress of Mathematicians, David Hilbert set out a list of 23 unsolved problems in mathematics. These problems, spanning many areas of mathematics, formed a central focus for much of 20th-century mathematics. Today, 10 have been solved, 7 are partially solved, and 2 are still open. The remaining 4 are too loosely formulated to be stated as solved or not.
Notable historical conjectures were finally proven. In 1976, Wolfgang Haken and Kenneth Appel used a computer to prove the four color theorem. Andrew Wiles, building on the work of others, proved Fermat's Last Theorem in 1995. Paul Cohen and Kurt Gödel proved that the continuum hypothesis is independent of (could neither be proved nor disproved from) thestandard axioms of set theory. In 1998 Thomas Callister Hales proved the Kepler conjecture.
A map illustrating the Four Color Theorem
The 20th century saw mathematics become a major profession. Every year, thousands of new Ph.D.s in mathematics were awarded, and jobs were available in both teaching and industry. An effort to catalogue the areas and applications of mathematics was undertaken in Klein's encyclopedia.
In a 1900 speech to the International Congress of Mathematicians, David Hilbert set out a list of 23 unsolved problems in mathematics. These problems, spanning many areas of mathematics, formed a central focus for much of 20th-century mathematics. Today, 10 have been solved, 7 are partially solved, and 2 are still open. The remaining 4 are too loosely formulated to be stated as solved or not.
Notable historical conjectures were finally proven. In 1976, Wolfgang Haken and Kenneth Appel used a computer to prove the four color theorem. Andrew Wiles, building on the work of others, proved Fermat's Last Theorem in 1995. Paul Cohen and Kurt Gödel proved that the continuum hypothesis is independent of (could neither be proved nor disproved from) thestandard axioms of set theory. In 1998 Thomas Callister Hales proved the Kepler conjecture.
21st century
In 2000, the Clay Mathematics Institute announced the seven Millennium Prize Problems, and in 2003 the Poincaré conjecture was solved by Grigori Perelman (who declined to accept an award on this point).
Most mathematical journals now have online versions as well as print versions, and many online-only journals are launched. There is an increasing drive towards open access publishing, first popularized by the arXiv.
In 2000, the Clay Mathematics Institute announced the seven Millennium Prize Problems, and in 2003 the Poincaré conjecture was solved by Grigori Perelman (who declined to accept an award on this point).
Most mathematical journals now have online versions as well as print versions, and many online-only journals are launched. There is an increasing drive towards open access publishing, first popularized by the arXiv.
